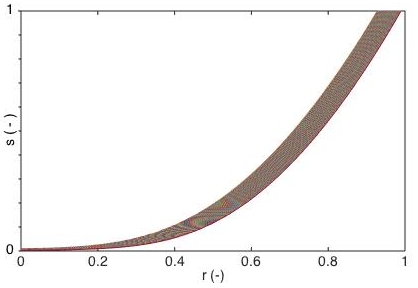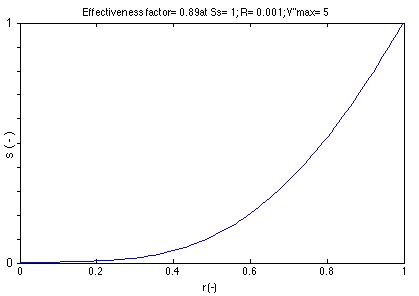The dimensionless substrate concentration was calculated as function of dimensionless distance (r) from the center of a homogeneous biocatalyst.
Left: Calculations that did not satify the criterion s=1 when r=1. Right hand graph shows the solution. See explanation below.

The substrate concentration gradient in a homogeneous bead with cells or enzyme consuming the substrate can be described with a second order differential equation that,  after conversion to dimensionless form, can be solved numerically.

This SIMSPEC file calculates the dimensionless relative susbtrate concentration in a homogeneous bead with a substrate consuming biocatalyst, assuming Monod kinetics. The calculation starts with an arbitrary concentration (s) at the bead center (r = 0) and steps gradually towards r=1. If s ≠ 1 when r = 1 is reached, the calculation starts again with a larger/smaller s at the center, and this procedure is repeated until s = 1 at r = 1 (see left hand graph). Then all incorrect gradients in the graph are eliminated (right hand graph), and the effectiveness factor is calculated. The effectiveness factor can be used to calculate the total reaction rate of the bead and from the bead concentration in the reactor the total reactor reaction rate can be obtained.

The theory of substrate diffusion limitation and its effect of the effectiveness factor (diffusion limited/ non-limited reaction rate) is included in Fermentation Process Engineering, 2nd ed. (will become available for downloading from www.enfors.eu).